NTAFTAWT

NTAFTAWT Details

Last update: 12-11-2007
This document describes the premise that "neurons that are fired together, are wired together".

Pattern Recognition

Seeing

The basic idea is to make some software that can recognize patterns.

The following image shows the representation of the eye connected to a single neuron.


Yes, eyes are not normally square, but it is easier to represent this way. Also natural eyes do not have this few of input sensors, so I guess this is closer to a model of a computer eye. The human eye has about 120 million rods and 6 million cones where the rods and cones have different characteristics. This representation borrows a few simple ideas from both types of sensors. Normally dendrites (inputs) are connected to axons (outputs), but since there is usually one axons for each neuron, these drawings will not show the axons.

An input pattern must be fed to the eye. The input pattern that will be fed initially is of solid blocks. One set of sensors will be fed a red (fired) block pattern, and the other set of sensors will be fed a green (non-fired) block pattern.


To get the neuron to learn a pattern, the dendrites must be mapped so that the neuron will fire when the dendrites connected to the sensors fire. So first, the neuron is initialized so that the dendrites randomly point to different sensors.


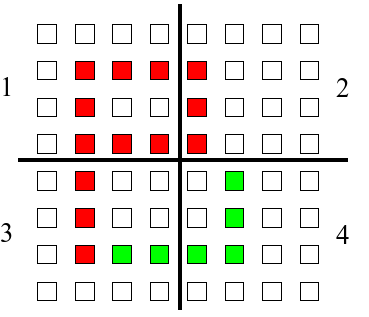
The colored blocks represent the sensors that are connected through dendrites to the neuron. The red blocks are the dendrites that have fired because they match the input pattern, and the green blocks are the dendrites that have not fired because the sensors were not fired in the input pattern. The white blocks are the sensors that are not connected to the neuron.

Learning

The basic idea is that as time goes by, the dendrites must be moved (remapped) so that they more closely match the input pattern. To do this, whenever a pattern is presented, the neuron will read the dendrite connections to see which ones have fired. The software will randomly pick one that has not fired and randomly choose a new location for the dendrite. It would be possible to search for a sensor that fired, but for now the dendrite is just randomly positioned. This leads to the first rule that neurons will be wired together when they fire closely in time. It may be possible to also use space at some point in the future. Since only dendrites that haven't fired are moved, eventually the dendrites will more closely match the input pattern. Each slice in time will move one dendrite. After one timeslice, the image may look like the following.


After a few more timeslices, the neuron will have more closely "learned" the input pattern.

One problem is that two dendrites from one neuron may end up being mapped to the same sensor. In a real brain this might not make a lot of sense since they would be in the same physical position. So for our purpose, there will be a rule that the software will only map the dendrite to a location where this neuron has not mapped to already.

There were experiments done on cats in the 1950's? that showed that when a cat's eye was covered after they were born for about two months, and then uncovered, the cat would never see again. This was because the neurons couldn't grow towards the cat's eyes. Hopefully they got a seeing eye dog for that cat. In any case, this is where the NTAFTAWT idea takes root.

This is very simple since there is only one neuron that only learned one pattern.

Learning Two Patterns

The next thing we try is four neurons with two patterns. The patterns will be the following.


At time 0, "Pattern 1" will be presented to the neurons. Then the neurons will map an unfired dendrite. At time 1, "Pattern 2" will be presented to the neurons. At time 3, "Pattern 1" will be presented. This will go on for some number of iterations.

One problem with this is that every other time, alternate sensors will be fired. That means that a dendrite that fired with one pattern could be remapped during the next pattern, and the neuron would never converge to one of the patterns. The solution is to make a new rule that there is a threshold where the number of dendrites that fired is used to determine whether to remap a dendrite that hasn't fired. If the threshold was not passed, no dendrites will be remapped.

If the threshold is set to 50%, then only when more than four sensors are fired, a dendrite will be remapped. The same threshold can be used to indicate whether a neuron has fired or not.

A graphical indication can be used to show whether a neuron has fired or not. After a random initialization, and with one pattern presented to the sensors, the neurons may look like the following.


The red indicates the neuron has fired, and the white indicates it has not fired. When the next pattern is presented, the neuron that has fired will no longer be fired because the dendrites will be looking at the non-fired sensors.

So this can now see two patterns, but is still too simple.

Learning Multiple Patterns

The next thing we try is 50 neurons with 26 patterns with a larger eye. You guessed it. The patterns are the 26 alphabetic characters.


One of the problems with these patterns is that some characters like the "I" have fewer sensors that will fire compared to the patterns like "W". This means that there needs to be a rule created for how to set the firing threshold.

The solution to this is to get the number of dendrites that are firing for each neuron, and set the fire threshold of so that only a certain number of neurons would fire with the current pattern. Then the learning/firing threshold will be set depending on how many neurons would fire at each threshold. of neurons will fire for each pattern.

This seems like it is using feedback, but it is much less of a problem than conventional neural networks. It is only using feed back from neighboring neurons. In conventional networks terminology, this would mean that they could even be in the same layer, and that feedback is not used between layers.

This can be implemented by using a histogram of the number of dendrites fired for each neuron, and then searching the histogram to find the neurons with the most dendrites that match the current pattern.

Another problem that can occur is that a neuron may never fire. So a rule is needed to eliminate dead neurons. If a neuron has passed quite a bit of time without ever firing, then a dendrite should be remapped. Eventually it should stumble across a pattern that will cause it to start firing.

So this can now see a few patterns and the future will definitely look brighter.

Converging to Patterns

One of the problems that comes up with the rules that exist so far, is that certain patterns will not converge and stick with a particular pattern. For example, the neuron may have dendrites that fire with the stem of a "P" character with a few dendrites firing on the other parts of the character. Then on a "K" pattern, the neuron will still fire on the stem, but then have other neurons that fire on the other parts of the character.


This means that it could oscillate between patterns. The firing threshold will not work in this case, because it is applied to all neurons, and this solution requires getting a particular neuron to bind to a pattern. The trick is simply to only remap a dendrite when it has more dendrites that match a pattern than the previous pattern that fired for that neuron. This way, it will start to bind to a pattern, and then converge more strongly to the pattern without shifting away when presented with a different pattern. This can be implemented by storing something with each dendrite that indicates the dendrite fired with the last pattern.

Learning Subset Patterns

Some characters are pure subsets of other characters. An example in some fonts is the I and J. In some fonts, it can be the "O" and "Q".


When a neuron converges on the subset character, it seems as if there is nothing to prevent it from learning and firing on the superset character. Rule 3 covers this problem well.

A large pattern may have many neurons that fire initially, and some neurons will converge to the pattern before others. Then when the superset pattern is presented again, the neurons that did not converge will not fire because they are below the threshold of the neurons that converged quickly, and are free to fire and learn with other patterns. This works well with Rule 4 to attempt to map some number of neurons to all patterns.

The fog is starting to lift, but we still have a ways to go.

Efficiency, Layers and Regions

If there was one neuron for every pattern presented to the eye, the number of neurons required would be astronomical. For example, a 4x4 set of elements would require 65536 (2 to the power 16) neurons to represent all possible patterns. And this only includes the binary on/off fired/non-fired patterns that we have used so far.

The simple answer is not to remember everything. Another answer is to use a hierarchical form of representation, which can be done using multiple layers of neurons, where each layer is separated into multiple regions. Many patterns will never occur, and some regions will be identical for multiple patterns.


Notice that region 1 can be the same for both the B and P characters. This means that a neuron with all of its dendrite connections can be the same. Using multiple layers of neurons would look something like the following.

If there are 4 regions of 2x2 elements, then there are 16 (2 to the power 4) combinations for each region * 4 regions. This means that 64 (16*4) neurons would represent all patterns, although there would be multiple neurons firing per pattern. The second layer can be fed the inputs from the first layer, and the neurons can represent many of the patterns.

There is a point in the eye where the optic nerve connects that has a blind spot. But when one eye is covered, you cannot see the blind spot. The brain does some type of "filling in" of the pattern. Perhaps this is one indication where it is possible to tell that not all input patterns are detectable by the brain.

You don't see what you think. I mean, you don't think what you see.

The Future